Vectors

Vectors and Direction

A study of motion will involve the introduction of a variety of quantities that are used to describe the physical world. Examples of such quantities include distance, displacement, speed, velocity, acceleration, force, mass, momentum, energy, work, power, etc. All these quantities can be divided into two categories - vectors and scalars. A vector quantity is a quantity that is fully described by both magnitude and direction. On the other hand, a scalar quantity is a quantity that is fully described by its magnitude. The emphasis of this unit is to understand some fundamentals about vectors and to apply the fundamentals in order to understand motion and forces that occur in two dimensions.

Each of these quantities are unique in that a full description of the quantity demands that both a magnitude and a direction are listed. For example, suppose your teacher tells you "A bag of gold is located outside the  classroom. To find it, displace yourself 20 meters." This statement may provide yourself enough information to pique your interest; yet, there is not enough information included in the statement to find the bag of gold. The displacement required to find the bag of gold has not been fully described. On the other hand, suppose your teacher tells you "A bag of gold is located outside the classroom. To find it, displace yourself from the center of the classroom door 20 meters in a direction 30 degrees to the west of north." This statement now provides a complete description of the displacement vector - it lists both magnitude (20 meters) and direction (30 degrees to the west of north) relative to a reference or starting position (the center of the classroom door). Vector quantities are not fully described unless both magnitude and direction are listed.


Vector quantities are often represented by scaled vector diagrams. Vector diagrams depict a vector by use of an arrow drawn to scale in a specific direction. Vector diagrams were introduced and used in earlier units 
to depict the forces acting upon an object. Such diagrams are commonly called as free-body diagrams. 



Representing the Magnitude of a Vector
The magnitude of a vector in a scaled vector diagram is depicted by the length of the arrow. The arrow is drawn a precise length in accordance with a chosen scale. For example, the diagram at the right shows a vector with a magnitude of 20 miles. Since the scale used for constructing the diagram is 1 cm = 5 miles, the vector arrow is drawn with a length of 4 cm. That is, 4 cm x (5 miles/1 cm) = 20 miles. Using the same scale (1 cm = 5 miles), a displacement vector that is 15 miles will be represented by a vector arrow that is 3 cm in length. Similarly, a 25-mile displacement vector is represented by a 5-cm long vector arrow. And finally, an 18-mile displacement vector is represented by a 3.6-cm long arrow. See the examples shown below.




In conclusion, vectors can be represented by use of a scaled vector diagram. On such a diagram, a vector arrow is drawn to represent the vector. The arrow has an obvious tail and arrowhead. The magnitude of a vector is represented by the length of the arrow. A scale is indicated (such as, 1 cm = 5 miles) and the arrow is drawn the proper length according to the chosen scale. The arrow points in the precise direction. 
Directions are described by the use of some convention. The most common convention is that the direction of a vector is the counterclockwise angle of rotation which that vector makes with respect to due East.

Vector Addition
A variety of mathematical operations can be performed with and upon vectors. One such operation is the addition of vectors. Two vectors can be added together to determine the result (or resultant). Observe the following summations of two force vectors:


These rules for summing vectors were applied to free-body diagrams in order to determine the net force (i.e., the vector sum of all the individual forces). Sample applications are shown in the diagram below.

In this unit, the task of summing vectors will be extended to more complicated cases in which the vectors are directed in directions other than purely vertical and horizontal directions. For example, a vector directed up and to the right will be added to a vector directed up and to the left. The vector sum will be determined for the more complicated cases shown in the diagrams below.

There are a variety of methods for determining the magnitude and direction of the result of adding two or more vectors. The two methods that will be discussed in this lesson and used throughout the entire unit 
are:

• the Pythagorean theorem and trigonometric methods
• the head-to-tail method using a scaled vector diagram

The Pythagorean Theorem

The Pythagorean theorem is a useful method for determining the result of adding two (and only two) vectors that make a right angle to each other. The method is not applicable for adding more than two vectors or for adding vectors that are not at 90-degrees to each other. The Pythagorean theorem is a mathematical equation that relates the length of the sides of a right triangle to the length of the hypotenuse of a right triangle.

To see how the method works, consider the following problem:

Eric leaves the base camp and hikes 11 km, north and then hikes 11 km east. Determine Eric's resulting displacement.

This problem asks to determine the result of adding two displacement vectors that are at right angles to each other. The result (or resultant) of walking 11 km north and 11 km east is a vector directed northeast as shown in the diagram to the right. Since the northward displacement and the eastward displacement are at right angles to each other, the Pythagorean theorem can be used to determine the resultant (i.e., the hypotenuse of the right triangle).

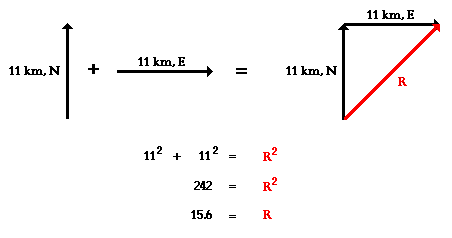
The result of adding 11 km, north plus 11 km, east is a vector with a magnitude of 15.6 km. Later, the method of determining the direction of the vector will be discussed.

Resultants

The resultant is the vector sum of two or more vectors. It is the result of adding two or more vectors together. If displacement vectors A, B, and C are added together, the result will be vector R. As shown in the diagram, vector R can be determined by the use of an accurately drawn, scaled, vector addition diagram.

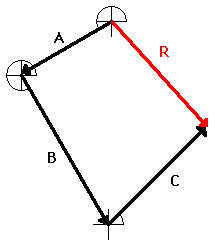
To say that vector R is the resultant displacement of displacement vectors A, B, and C is to say that a person who walked with displacements A, then B, and then C would be displaced by the same amount as a person who walked with displacement R. Displacement vector R gives the same result as displacement vectors A + B + C. That is why it can be said that

A + B + C = R

In situations in which vectors are directed at angles to the customary coordinate axes, a useful mathematical trick will be employed to transform the vector into two parts with each part being directed along the coordinate axes. For example, a vector that is directed northwest can be thought of as having two parts - a northward part and a westward part. A vector that is directed upward and rightward can be thought of as having two parts - an upward part and a rightward part.

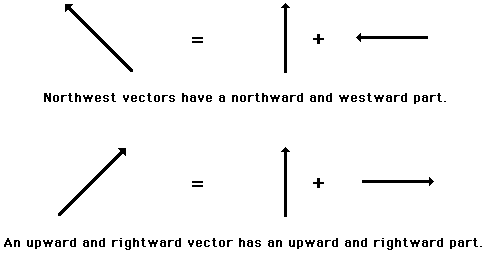
Any vector directed in two dimensions can be thought of as having an influence in two different directions. That is, it can be thought of as having two parts. Each part of a two-dimensional vector is known as a component. The components of a vector depict the influence of that vector in a given direction. The combined influence of the two components is equivalent to the influence of the single two-dimensional vector. The single two-dimensional vector could be replaced by the two components.

If Fido's dog chain is stretched upward and rightward and pulled tight by his master, then the tension force in the chain has two components - an upward component and a rightward component. To Fido, the influence of the chain on his body is equivalent to the influence of two chains on his body - one pulling upward and the other pulling rightward. If the single chain were replaced by two chains. with each chain having the magnitude and direction of the components, then Fido would not know the difference. This is not because Fido is dumb (a quick glance at his picture reveals that he is certainly not that), but rather because the combined influence of the two components is equivalent to the influence of the single two-dimensional vector.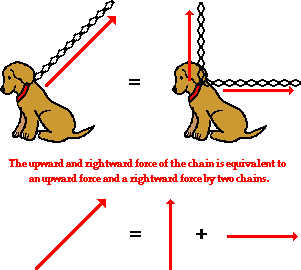

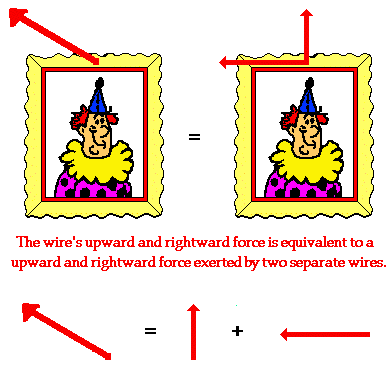
 Consider a picture that is hung to a wall by means of two wires that are stretched vertically and horizontally. Each wire exerts a tension force upon the picture to support its weight. Since each wire is stretched in two dimensions (both vertically and horizontally), the tension force of each wire has two components - a vertical component and a horizontal component. Focusing on the wire on the left, we could say that the wire has a leftward and an upward component. This is to say that the wire on the left could be replaced by two wires, one pulling leftward and the other pulling upward. If the single wire were replaced by two wires (each one having the magnitude and direction of the components), then there would be no affect upon the stability of the picture. The combined influence of the two components is equivalent to the influence of the single two-dimensional vector.

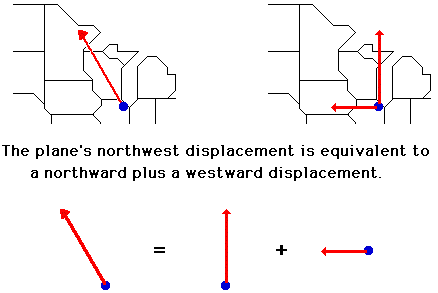
Consider an airplane that is flying from Chicago's O'Hare International Airport to a destination in Canada. Suppose that the plane is flying in such a manner that its resulting displacement vector is northwest. If this is the case, then the displacement of the plane has two components - a component in the northward direction and a component in the westward direction. This is to say that the plane would have the same displacement if it were to take the trip into Canada in two segments - one directed due North and the other directed due West. If the single displacement vector were replaced by these two individual displacement vectors, then the passengers in the plane would end up in the same final position. The combined influence of the two components is equivalent to the influence of the single two-dimensional displacement.

Any vector directed in two dimensions can be thought of as having two different components. The component of a single vector describes the influence of that vector in a given direction.

APPLICATIONS OF VECTORS IN EVERYDAY LIFE

There are lots of things related to vectors. Examples are airline pilots, sea captains, doctors tracking the progress of an epidemic, meteorologists tracking weather systems, engineers of every kind dealing with forces and motion, scientists, astronauts, etc.

In everyday life, from waking up we already encounter these things. From your bed you go to the bathroom then back to your room, then to the kitchen. Walking alone is related to vectors. Also, when we run and drive, these things involve both magnitude and direction - which are vector quantities. 

Free Fall motion

Introduction to Free Fall
A free falling object is an object that is falling under the sole influence of gravity. Any object that is being acted upon only by the force of gravity is said to be in a state offree fall. There are two important motion characteristics that are true of free-falling objects:

• Free-falling objects do not encounter air resistance.

• All free-falling objects (on Earth) accelerate downwards at a rate of 9.8 m/s/s (often approximated as 10 m/s/s for back-of-the-envelope calculations)

Because free-falling objects are accelerating downwards at a rate of 9.8 m/s/s, a ticker tape trace or dot diagram of its motion would depict an acceleration. The dot diagram at the right depicts the acceleration of a free-falling object. The position of the object at regular time intervals - say, every 0.1 second - is shown. The fact that the distance that the object travels every interval of time is increasing is a sure sign that the ball is speeding up as it falls downward.
Free-fall acceleration is often witnessed in a physics classroom by means of an ever-popular strobe light demonstration. The room is darkened and a jug full of water is connected by a tube to a medicine dropper. The dropper drips water and the strobe illuminates the falling droplets at a regular rate - say once every 0.2 seconds. Instead of seeing a stream of water free-falling from the medicine dropper, several consecutive drops with increasing separation distance are seen. The pattern of drops resembles the dot diagram shown in the graphic at the right.

The Kinematic Equations

The kinematic equations are a set of four equations that can be utilized to predict unknown information about an object's motion if other information is known. The equations can be utilized for any motion that can be described as being either a constant velocity motion (an acceleration of 0 m/s/s) or a constant acceleration motion. They can never be used over any time period during which the acceleration is changing. Each of the kinematic equations include four variables. If the values of three of the four variables are known, then the value of the fourth variable can be calculated. In this manner, the kinematic equations provide a useful means of predicting information about an object's motion if other information is known. For example, if the acceleration value and the initial and final velocity values of a skidding car is known, then the displacement of the car and the time can be predicted using the kinematic equations.

Kinematic Equations and Free Fall

As mentioned, a free-falling object is an object that is falling under the sole influence of gravity. That is to say that any object that is moving and being acted upon only be the force of gravity is said to be "in a state of free fall." Such an object will experience a downward acceleration of 9.8 m/s/s. Whether the object is falling downward or rising upward towards its peak, if it is under the sole influence of gravity, then its acceleration value is 9.8 m/s/s.

Like any moving object, the motion of an object in free fall can be described by four kinematic equations. The kinematic equations that describe any object's motion are:

The symbols in the above equation have a specific meaning: the symbol d stands for the displacement; the symbol tstands for the time; the symbol a stands for the acceleration of the object (gravitational acceleration: -9.8m/s/s); the symbol v_i stands for the initial velocity value; and the symbol v_f stands for the final velocity.

There are a few conceptual characteristics of free fall motion that will be of value when using the equations to analyze free fall motion. These concepts are described as follows:

• An object in free fall experiences an acceleration of -9.8 m/s/s. (The - sign indicates a downward acceleration.) Whether explicitly stated or not, the value of the acceleration in the kinematic equations is -9.8 m/s/s for any freely falling object.
• If an object is merely dropped (as opposed to being thrown) from an elevated height, then the initial velocity of the object is 0 m/s.
• If an object is projected upwards in a perfectly vertical direction, then it will slow down as it rises upward. The instant at which it reaches the peak of its trajectory, its velocity is 0 m/s. This value can be used as one of the motion parameters in the kinematic equations; for example, the final velocity (v_f) after traveling to the peak would be assigned a value of 0 m/s.
• If an object is projected upwards in a perfectly vertical direction, then the velocity at which it is projected is equal in magnitude and opposite in sign to the velocity that it has when it returns to the same height. That is, a ball projected vertically with an upward velocity of +30 m/s will have a downward velocity of -30 m/s when it returns to the same height.

These four principles and the four kinematic equations can be combined to solve problems involving the motion of free falling objects.

(source:  http://www.physicsclassroom.com/class/1DKin/U1L6a.cfm  )

Graphs of how the position, velocity, and acceleration of objects under free fall motion change in time follow.

Figure 2.3: Free fall acceleration

Figure 2.4: Free fall velocity

Figure 2.5: Free fall position

Problems :)  

Example The boy drops the ball from a roof of the house which takes 3 seconds to hit the ground. Calculate the velocity before the ball crashes to the ground. (g=10m/s² (9.8m/s² )

Velocity is;

V=g.t

V=10m/ s².3s=30m/s

We have learned how to find the velocity of the object at a given time. Now we will learn how to find the distance taken during the motion. I give some equations to calculate distance and other quantities. Galileo found an equation for distance from his experiments. 

This equation is;

Using this equation we can find the height of the house in given example above. Let’s found how height the ball has been dropped? We use 10 m/s² for g.

I think the formula now a little bit clearer in your mind. We will solve more problems related to this topic. Now, think that if I throw the ball straight upward with an initial velocity. When it stops and falls back to the ground? We answer these questions now. 

Picture shows the magnitudes of velocity at the bottom and at the top. As you can see the ball is thrown upward with an initial v velocity, at the top it’s velocity becomes zero and it changes it’s direction and starts to fall down which is free fall. Finally at the bottom before the crash it reaches its maximum speed which shown as V’. We have talked about the amount of increase in the velocity in free fall. It increases 9,8m/s in each second due to the gravitational acceleration. In this case, there is also g but the ball’s direction is upward; so the sign of g is negative. Thus, our velocity decreases in 9,8m/s in each second until the velocity becomes zero. At the top, because of the zero velocity, the ball changes its direction and starts to free fall. Before solving problems I want to give the graphs of free fall motion.

As you see in the graphs our velocity is linearly increases with an acceleration “g”, second graphs tells us that acceleration is constant at 9,8m/s², and finally third graphic is the representation of change in our position. At the beginning we have a positive displacement and as the time passes it decreases and finally becomes zero. Now we can solve problems using these graphs and explanations. 

Example John throws the ball straight upward and after 1 second it reaches its maximum height then it does free fall motion which takes 2 seconds. Calculate the maximum height and velocity of the ball before it crashes the ground. (g=10m/s²)

(source: http://www.physicstutorials.org/home/mechanics/1d-kinematics/free-fall)